4. Convex mixture of m-randomized checkerboards

Introduction

In this vignette, we will demonstrate how the checkerboard parameters $m$ can be used to produce an efficient meta-model. We will construct $m$ -randomized checkerboard copulas, and based on some fit statistics we will then combine them in a convex mixture. Our model here will use all possibles $m_i$ ’s values for checkerboard copulas and aggregate all those values by optimizing a quadratic loss under resampling condition. As usual, we will work on the LifeCycleSavings dataset :

set.seed(1)
df <- apply(LifeCycleSavings,2,rank)/(nrow(LifeCycleSavings)+1)
d = ncol(df)
n = nrow(df)
nb_replicates = 20 # number of replication of the resampling.
nb_fold = 5 # "k" value for the k-fold resampling method.
nb_cop = 50 # the number of m-randomized checkerboard copulas we will test.
pairs(df,lower.panel = NULL)

Fitting function

The following functions proposes a fit :


make_k_fold_samples <- function(data,k = nb_fold,n_repeat = 1){
  
  sapply(1:n_repeat,function(n){
      # shuffle data : 
      data <- data[sample(nrow(data)),]
    
      # create k folds : 
      folds <- cut(seq(1,nrow(data)),breaks=k,labels=FALSE)
      
      sapply(1:k,function(i){
        test_index <- which(folds==i,arr.ind=TRUE)
        return(list(train = data[-test_index,], 
                    test = data[test_index,]))
      },simplify=FALSE)
  })
}

build_random_m <- function(how_much=1,dim = d,nrow_data){
  t(sapply(1:how_much,function(i){
    m_pos = (2:nrow_data)[nrow_data%%(2:nrow_data)==0]
    sample(m_pos,d,replace=TRUE)
  }))
}

build_all_checkerboard <- function(sampled_data,m){
  lapply(sampled_data,function(d){
    apply(m,1,function(m_){
      cbCopula(x = d$train,m = m_,pseudo=TRUE)
    })
  })
}

samples <- make_k_fold_samples(df,k=nb_fold,n_repeat=nb_replicates)
rand_m <- build_random_m(nb_cop,d,nrow(samples[[1]]$train))
cops <- build_all_checkerboard(samples,rand_m)

Let’s first calculate the empirical copula values :

pEmpCop <- function(points,data=df){
  sapply(1:nrow(points),function(i){
    sum(colSums(t(data) <= points[i,]) == d)
  }) / nrow(data)
}

Now, we also need to calculate the errors that our copulas made compared to the empirical copula (our benchmark).

error <- function(cop,i,j){
  test <- samples[[i]]$test
  return(sum((pCopula(test,cop) - pEmpCop(test))^2))
  
}

errors <- sapply(1:(nb_replicates*nb_fold),function(i){
  sapply(1:nb_cop,function(j){
   error(cops[[i]][[j]],i,j)
  })
})

rmse_by_model <- sqrt(rowMeans(errors))
plot(rmse_by_model)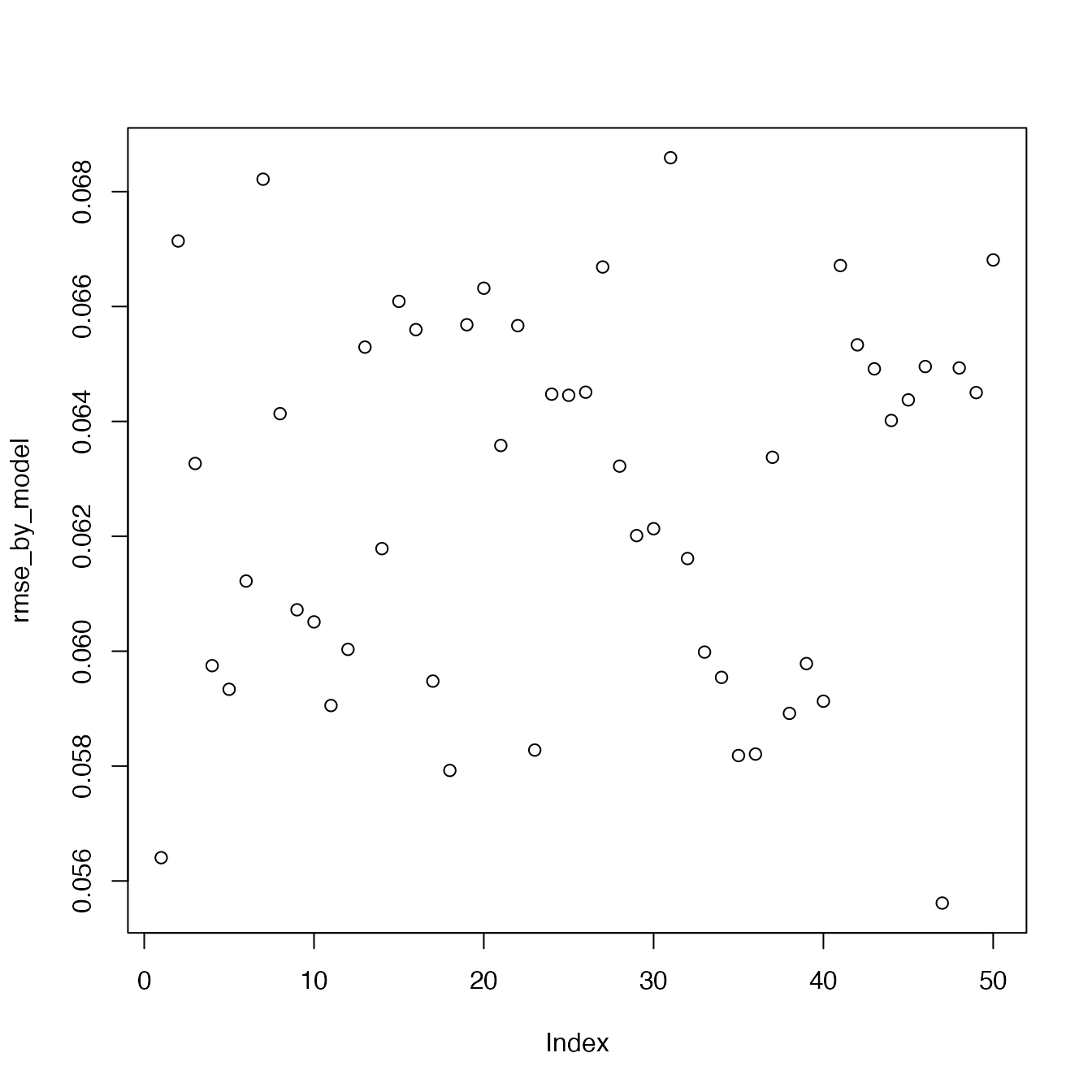

Each point on the graph correspond to the rmse of a model. We recall the values of $m$ used by those models :

rand_m
#>       [,1] [,2] [,3] [,4] [,5]
#>  [1,]   10    2    5    8   10
#>  [2,]    5   40    8    5    4
#>  [3,]    2    4   20   40    8
#>  [4,]   20   10    5    5    4
#>  [5,]    4    2   10   40    8
#>  [6,]    4   40    4    5   10
#>  [7,]    5   10   40    8    2
#>  [8,]   20   20   40   10   10
#>  [9,]    2   20    2   20   40
#> [10,]    4    5    4   20    5
#> [11,]   20    5    2    2    8
#> [12,]   40    2   20   40   40
#> [13,]   40    8    8   40    2
#> [14,]    2    2   40    4    2
#> [15,]    2   10   10    2    4
#> [16,]    2    4   20   10    2
#> [17,]    8    8    4   10   20
#> [18,]    4    5    2    2   10
#> [19,]    8   20   20    2   40
#> [20,]    4   40   40    2    5
#> [21,]    4    5   40   20    4
#> [22,]    2   20    8    8   40
#> [23,]   40    2    2   40   10
#> [24,]    8    4   40   20   10
#> [25,]   20   10    8    5   20
#> [26,]   40   10   40   40   10
#> [27,]    4    5   40    2    2
#> [28,]   20    5   10   40    4
#> [29,]   40   10    2   40    5
#> [30,]    5    5    4   40    5
#> [31,]    5   20   40    8   40
#> [32,]    5   10    5   10   10
#> [33,]   10   10    2   10    5
#> [34,]    2   20    2    8    4
#> [35,]    2    2    8    5   20
#> [36,]    5    2    8   10   10
#> [37,]    2    5   10    5   40
#> [38,]   10    5    4   10   20
#> [39,]   10    8    4   40   10
#> [40,]   20   10    2    2    2
#> [41,]    5    8   40    8   40
#> [42,]   40   40   40   40   10
#> [43,]    8    4   40    2    5
#> [44,]   20   40    8    2    4
#> [45,]    2    4   20    4    8
#> [46,]   40   20   40   20   10
#> [47,]   40    2   20   10    8
#> [48,]    4    8   20    8   40
#> [49,]   40   40   20   20   10
#> [50,]    5   40    4    8    2

convex_combination <- ConvexCombCopula(unlist(cops,recursive=FALSE),alpha = rep(1/rmse_by_model,nb_replicates*nb_fold))
simu = rCopula(1000,convex_combination)
pairs(simu,lower.panel = NULL,cex=0.5)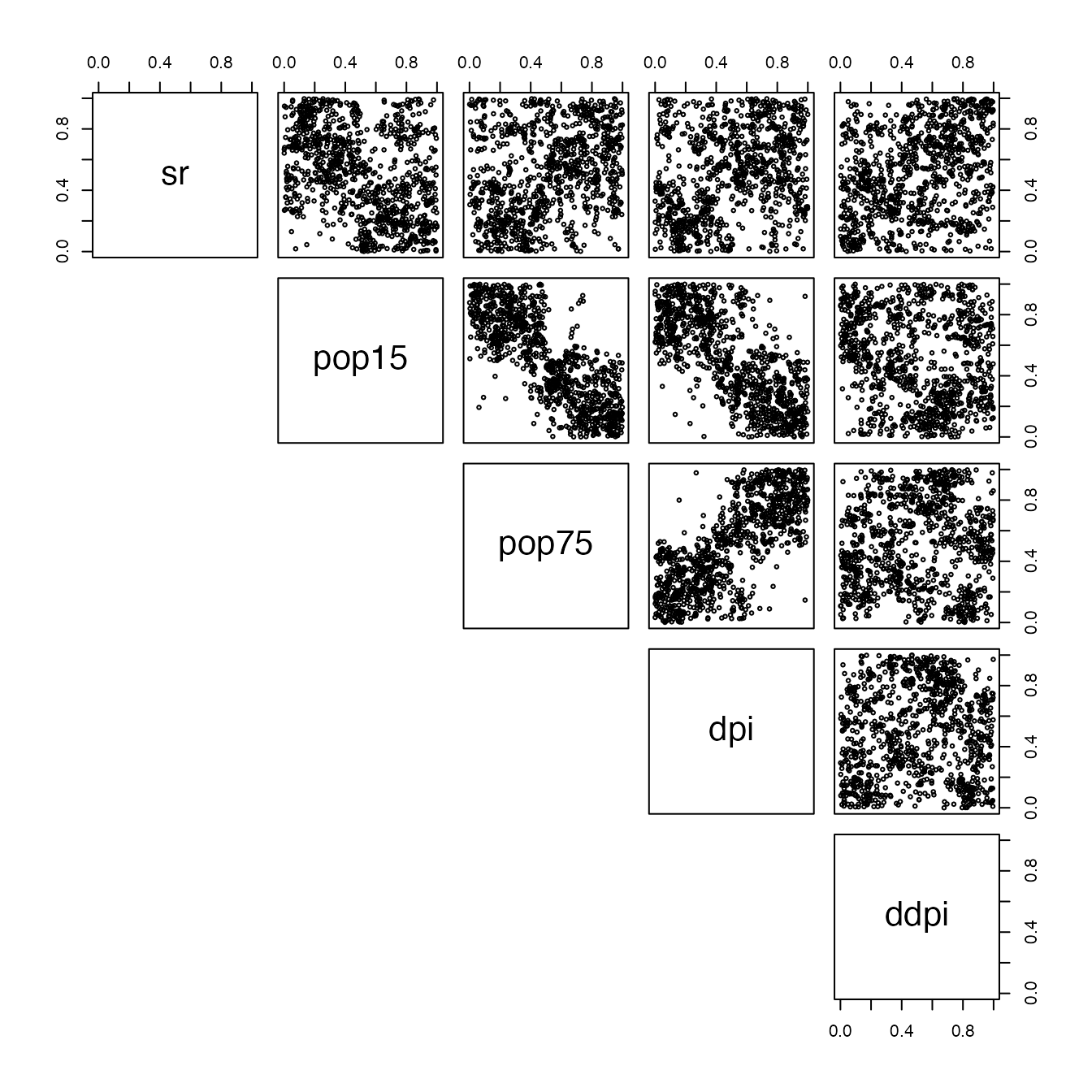

Which is quite good compared to the dataset we started with. This process is really fast and useful, and can of course be used for high-dimensional datasets.

The parameters nb_fold, nb_repeats, nb_cop could be further optimized. Furthermore, if some multivariate margins are known, the same thing could be done using cbkmCopula() instead of cbCopula() models.

Oskar Laverny

2024-12-26

Introduction

Fitting function