Copulas and Sklar Distributions

This section gives some general definitions and tools about dependence structures, multivariate random vectors and copulas. Along this journey through the mathematical theory of copulas, we link to the rest of the documentation for more specific and detailed arguments on particular points, or simply to the technical documentation of the actual implementation. The interested reader can take a look at the standard books on the subject [1–4] or more recently [5–8].

We start here by defining a few concepts about multivariate random vectors, dependence structures and copulas.

Reminder on multivariate random vectors

Consider a real valued random vector $\mathit{X}=(X_1,...,X_d):\mathrm{\Omega }\to {\mathbb{R}}^d$. The random variables $X_1,...,X_d$ are called the marginals of the random vector $\mathit{X}$.

Info: Constructing random variables in Julia via `Distributions.jl`

Recall that you can construct random variables in Julia by the following code :

using Distributions
X₁ = Normal()       # A standard Gaussian random variable
X₂ = Gamma(2,3)     # A Gamma random variable
X₃ = Pareto(1)      # A Pareto random variable with infinite variance.
X₄ = LogNormal(0,1) # A Lognormal random variable

We refer to Distributions.jl's documentation for more details on what you can do with these objects. We assume here that you are familiar with their API.

The probability distribution of the random vector $\mathit{X}$ can be characterized by its distribution function $F$:

$$\begin{array}{rl}F(\mathit{x})& =\mathbb{P}(\mathit{X}\le \mathit{x})\\ & =\mathbb{P}(\mathrm{\forall }i\in \{1,...,d\},X_i\le x_i).\end{array}$$

For a function $F$ to be the distribution function of some random vector, it should be $d$-increasing, right-continuous and left-limited. For $i\in \{1,...,d\}$, the random variables $X_1,...,X_d$, called the marginals of the random vector, also have distribution functions denoted $F_1,...,F_d$ and defined by :

$$F_i(x_i)=F(+\mathrm{\infty },...,+\mathrm{\infty },x_i,+\mathrm{\infty },...,+\mathrm{\infty }).$$

Note that the range $\mathrm{Ran}(F)$ of a distribution function $F$, univariate or multivariate, is always contained in $[0,1]$. When the random vector or random variable is absolutely continuous with respect to (w.r.t.) the Lebesgue measure restricted to its domain, the range is exactly $[0,1]$. When the distribution is discrete with $n$ atoms, the range is a finite set of $n+1$ values in $[0,1]$.

Copulas and Sklar's Theorem

There is a fundamental functional link between the function $F$ and its marginals $F_1,...,F_d$. This link is expressed by the mean of copulas.

Definition: Copula

A copula, usually denoted $C$, is the distribution function of a random vector with marginals that are all uniform on $[0,1]$, i.e.

$$C_i(u)=u{\mathbb{1}}_{u\in [0,1]}\text{ for all }i\in 1,...,d.$$

Info: Vocabulary

In this documentation but more largely in the literature, the term Copula refers both to the random vector and its distribution function. Usually, the distinction is clear from context.

You may define a copula object in Julia by simply calling its constructor:

using Copulas
d = 3 # The dimension of the model
θ = 7 # Parameter
C = ClaytonCopula(d,7) # A 3-dimensional clayton copula with parameter θ = 7.

ClaytonCopula{3, Float64}(θ = 7.0,)

This object is a random vector, and behaves exactly as you would expect a random vector from Distributions.jl to behave: you may sample it with rand(C,100), compute its pdf or cdf with pdf(C,x) and cdf(C,x), etc:

u = rand(C,10)

3×10 Matrix{Float64}:
 0.526499  0.021291   0.328704  0.378685  …  0.00930735  0.435106  0.639032
 0.185059  0.0198878  0.327653  0.634566     0.0101885   0.314647  0.717941
 0.230508  0.0245785  0.407804  0.440913     0.0122688   0.391426  0.831335

cdf(C,u)

10-element Vector{Float64}:
 0.1799684597482713
 0.018217998740626747
 0.29288020390502756
 0.36205242045170244
 0.14000537176743774
 0.2035742447106413
 0.47338044958092873
 0.008645801678165276
 0.30242231253926444
 0.6022595816237779

You can also plot it:

using Plots
plot(C, :logpdf)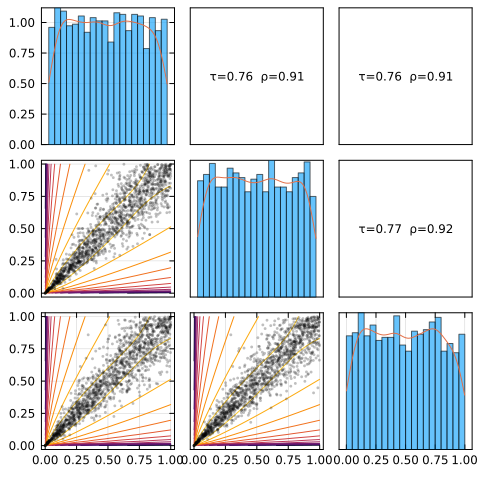

See the visualizations page for details on the visualisations tools. It’s often useful to get an intuition by looking at scatter plots.

Example: Independence

To give another example, the function

$$\mathrm{\Pi }:\mathit{x}\mapsto \prod _{i=1}^d{x}_i={\mathit{x}}^{\mathbf{1}}$$

is a copula, corresponding to independent random vectors.

This copula can be constructed using the IndependentCopula(d) syntax as follows:

Π = IndependentCopula(d) # A 4-variate independence structure.

One of the reasons that makes copulas so useful is the bijective map from the Sklar Theorem [9]:

Theorem: Sklar (1959)

For every random vector $\mathit{X}$, there exists a copula $C$ such that

$$\mathrm{\forall }\mathit{x}\in {\mathbb{R}}^d,F(\mathit{x})=C(F_1(x_1),...,F_d(x_d)).$$

The copula $C$ is uniquely determined on $\mathrm{Ran}(F_1)\times ...\times \mathrm{Ran}(F_d)$, where $\mathrm{Ran}(F_i)$ denotes the range of the function $F_i$. In particular, if all marginals are absolutely continuous, $C$ is unique.

This result allows to decompose the distribution of $\mathit{X}$ into several components: the marginal distributions on one side, and the copula on the other side, which governs the dependence structure between the marginals. This object is central in our work, and therefore deserves a moment of attention.

We can then leverage the Sklar theorem to construct multivariate random vectors from a copula-marginals specification. The implementation we have of this theorem allows building multivariate distributions by specifying separately their marginals and dependence structures as follows:

X₁, X₂, X₃ = Gamma(2,3), Pareto(), LogNormal(0,1) # Marginals
D = SklarDist(C, (X₁,X₂,X₃)) # The final distribution, using the previous copula C.
plot(D, scale=:sklar)

The obtained multivariate random vector object are genuine multivariate random vector following the Distributions.jl API. They can be sampled (rand()), and their probability density function and distribution function can be evaluated (respectively pdf and cdf), etc:

x = rand(D,10)
p = pdf(D, x)
l = logpdf(D, x)
c = pdf(D, x)
[x' p l c]

10×6 Matrix{Float64}:
  6.69517    5.58109   1.17787    0.0017726    -6.33531    0.0017726
  1.18882    1.10947   0.247609   1.71045       0.536758   1.71045
  1.49555    1.10542   0.261395  21.8693        3.08508   21.8693
 10.5131    36.1181    2.18118    2.15652e-5  -10.7444     2.15652e-5
  5.49422    2.75962   1.18787    0.0368705    -3.30034    0.0368705
  4.36807    2.5307    0.874563   0.0350585    -3.35074    0.0350585
  3.79386    1.64029   0.826916   0.374565     -0.981991   0.374565
  1.77016    1.17064   0.283964   3.74605       1.3207     3.74605
  1.00082    1.06406   0.219168   6.68743       1.90023    6.68743
 15.6653   223.158    13.6095     1.25381e-8  -18.1945     1.25381e-8

Sklar's theorem can be used the other way around (from the marginal space to the unit hypercube): this is, for example, what the pseudo() function does, computing ranks.

Info: Independent random vectors

Distributions.jl provides the product_distribution function to create independent random vectors with given marginals. product_distribution(args...) is essentially equivalent to SklarDist(IndependentCopula(d), args), but our approach generalizes to other dependence structures.

Copulas are bounded functions with values in [0,1] since they correspond to probabilities. But their range can be bounded more precisely, and [10] gives us:

Property: Fréchet-Hoeffding bounds

For all $\mathit{x}\in [0,1{]}^d$, every copula $C$ satisfies :

$$⟨\mathbf{1},\mathit{x}-1+d^{-1}{⟩}_{+}\le C(\mathit{x})\le min\mathit{x},$$

where $y_{+}=max(0,y)$.

The function $M:\mathit{x}\mapsto min\mathit{x}$, called the upper Fréchet-Hoeffding bound, is a copula. The function $W:\mathit{x}\mapsto ⟨\mathbf{1},\mathit{x}-1+d^{-1}{⟩}_{+}$, called the lower Fréchet-Hoeffding bound, is on the other hand a copula only when $d=2$. These two copulas can be constructed through MCopula(d) and WCopula(2).

The upper Fréchet-Hoeffding bound corresponds to the case of comonotone random vector: a random vector $\mathit{X}$ is said to be comonotone, i.e., to have copula $M$, when each of its marginals can be written as a non-decreasing transformation of the same random variable (say with $\mathcal{U}([0,1])$ distribution). This is a simple but important dependence structure. See e.g.,[11, 12] on this particular copula.

Here is a plot of the independence, a positive dependence (Clayton), and the Fréchet bounds in bivariate cases. You can visualize the strong alignment for M and the anti-diagonal pattern for W.

p1 = plot(IndependentCopula(2), title="IndependentCopula(2)")
p2 = plot(ClaytonCopula(2, 3.0), title="ClaytonCopula(2, 3.0)")
p3 = plot(MCopula(2), title="MCopula(2)")
p4 = plot(WCopula(2), title="WCopula(2)")
plot(p1,p2,p3,p4; layout=(2,2), size=(800,600))

Since copulas are distribution functions, like distribution functions of real-valued random variables and random vectors, there exists classical and useful parametric families of copulas (we already saw the Clayton family). You can browse the available families in this package in the Bestiary. Like any families of random variables or random vectors, copulas are fittable on empirical data.

A tour of the main API

The public API of Copulas.jl is quite small and easy to expose on a simple example, which is what we will do right now.

Copulas and SklarDist

The most important objects of the package are of course copulas as sklar distributions. Both of these objects follow the Distributions.jl's API, and so you can construct, sample, and evaluate copulas as standard Distributions.jl objects:

using Copulas, Distributions, Random, StatsBase
C = ClaytonCopula(3, 2.0)
u = rand(C, 5)
Distributions.loglikelihood(C, u)

4.027995257604113

X₁, X₂, X₃ = Gamma(2,3), Beta(1,5), LogNormal(0,1)
C2 = GumbelCopula(3, 1.7)
D = SklarDist(C2, (X₁, X₂, X₃))
rand(D, 3)
pdf(D, rand(3))

5.661469705639546e-6

Basic dependence metrics.

Basic dependence summaries available on copulas, whatever their dimension d:

multivariate_stats = (
    kendall_tau = Copulas.τ(C),
    spearm_rho = Copulas.ρ(C),
    blomqvist_beta = Copulas.β(C),
    gini_gamma = Copulas.γ(C),
    entropy_iota = Copulas.ι(C),
    lower_tail_dep = Copulas.λₗ(C),
    upper_tail_dep = Copulas.λᵤ(C)
)

(kendall_tau = 0.5, spearm_rho = 0.6822338331574409, blomqvist_beta = 0.19419223902606517, gini_gamma = 0.5239426802975992, entropy_iota = -0.9637828011396714, lower_tail_dep = 0.5773502691896257, upper_tail_dep = 0.0)

The same functions have dispatches for u::Abstractmatrix of size (d,d) where d is the dimension of the copula and n is the number of observations, which provide sample versions of the same quantities. Moreover, since most of these statistics are more common in bivariate case, we provide the folllowing bindings for pairwise matrices of the same dependence metrics:

StatsBase.corkendall(C)
StatsBase.corspearman(C)
Copulas.corblomqvist(C)
Copulas.corgini(C)
Copulas.corentropy(C)
Copulas.corlowertail(C)
Copulas.coruppertail(C)

3×3 Matrix{Float64}:
 1.0  0.0  0.0
 0.0  1.0  0.0
 0.0  0.0  1.0

and of course once again the same functions dispatch on u::Abstractmatrix, but, for historical reasons, they require dataset to be (n,d)-shaped and not (d,n), so you have to transpose.

Measure function

A measure function gives the measure of hypercubes from any copula as follows:

Copulas.measure(C, (0.1,0.2,0.3), (0.9,0.8,0.7))

0.27586746224441333

Subsetting (working with a subset of dimensions)

Extract lower-dimensional dependence without materializing new data:

S23 = subsetdims(C2, (2,3))  # a bivariate copula view
StatsBase.corkendall(S23)

2×2 Matrix{Float64}:
 1.0       0.411765
 0.411765  1.0

For Sklar distributions, subsetting returns a smaller joint distribution:

D13 = subsetdims(D, (1,3))
rand(D13, 2)

2×2 Matrix{Float64}:
 1.41983  0.128844
 1.00023  0.288662

Conditioning (conditional marginals and joint conditionals)

On the uniform scale (copula): distortions and conditional copulas are provided:

Dj = condition(C2, 2, 0.3)   # Distortion of U₁|U₂=0.3 when d=2
Distributions.cdf(Dj, 0.95)

0.9896065697045947

On the original scale (Sklar distribution):

Dc = condition(D, (2,3), (0.3, 0.2))
rand(Dc, 2)

2-element Vector{Float64}:
 1.457043991260875
 2.742608160612362

And rosenblatt transfromations of the copula (or sklardist) can be obtained as follows:

u = rand(D, 10)
s = rosenblatt(D, u)
u2 = inverse_rosenblatt(D, s)
maximum(abs, u2 .- u) # should be approx zero.

9.547918011776346e-14

These transformation leverage the conditioning mechanismes.

Fitting (copulas and Sklar distributions)

You can fit copulas from pseudo-observations U, and Sklar distributions from raw data X. Available methods vary by family; see the fitting manual for details.

X = rand(D, 500)
M = fit(CopulaModel, SklarDist{GumbelCopula, Tuple{Gamma,Beta,LogNormal}}, X; copula_method=:mle)

────────────────────────────────────────────────────────────────────────────────
[ CopulaModel: SklarDist ] (Copula=Archimedean d=3, Margins=(Gamma, Beta, LogNormal))
────────────────────────────────────────────────────────────────────────────────
Copula:                Archimedean d=3
Margins:               (Gamma, Beta, LogNormal)
Methods:               copula=mle, sklar=ifm
Number of observations: 500
────────────────────────────────────────────────────────────────────────────────
[ Fit metrics ]
────────────────────────────────────────────────────────────────────────────────
Null Loglikelihood:      -1638.2407
Loglikelihood:           -1304.8881
LR (vs indep.):        666.71 ~ χ²(1)  ⇒  p = <1e-16
AIC:                   2611.776
BIC:                   2615.991
Converged:             true
Iterations:            3
Elapsed:               0.045s
────────────────────────────────────────────────────────────────────────────────
[ Dependence metrics ]
────────────────────────────────────────────────────────────────────────────────
Kendall τ:             0.4304
Spearman ρ:            0.6002
Blomqvist β:           0.1311
Gini γ:                0.4539
Upper λᵤ:              0.4173
Lower λₗ:              0.0000
Entropy ι:             -0.6683
────────────────────────────────────────────────────────────────────────────────
[ Copula parameters ] (vcov=hessian)
────────────────────────────────────────────────────────────────────────────────
Parameter    Estimate   Std.Err   z-value    p-val     95% Lo     95% Hi
θ              1.7555    0.0439    40.004   <1e-16     1.6695     1.8415
────────────────────────────────────────────────────────────────────────────────
[ Marginals ]
────────────────────────────────────────────────────────────────────────────────
Margin Dist       Param    Estimate   Std.Err 95% CI
#1     Gamma      α          2.1205    0.1250 [1.8755, 2.3655]
                  θ          2.8686    0.1907 [2.4949, 3.2423]
#2     Beta       α          0.9715    0.0541 [0.8654, 1.0775]
                  β          4.8205    0.3262 [4.1811, 5.4598]
#3     LogNormal  μ         -0.0175    0.0449 [-0.1055, 0.0706]
                  σ          1.0046    0.0318 [0.9422, 1.0670]

A shortcut allows to directly get the fitting object (copula or sklardist) by simply ommiting the first CopulaModel argument:

U = pseudos(X)
Ĉ = fit(GumbelCopula, U; method=:itau)
Copulas.τ(Ĉ)

0.4240184837401018

Notes:

• fit chooses a reasonable default per-family; pass method/copula_method to control it.

• Common copula methods include :mle, :itau, :irho, :ibeta; for Sklar fitting, :ifm (parametric CDFs) and :ecdf (pseudo-observations) are available.

• CopulaModel implements model stats: nobs, coef, vcov, stderror, confint, aic/bic, nullloglikelihood, and more.

• For a Bayesian workflow over Sklar models, see the examples section.

Info: About fitting procedures

The Distributions.jl documentation states:

The fit function will choose a reasonable way to fit the distribution, which, in most cases, is maximum likelihood estimation.

We embrace this philosophy: from one copula family to another, the default fitting method may differ. Treat fit as a quick starting point; when you need control, specify method/copula_method explicitly.

Next steps

The documentation of this package aims to combine theoretical information and references to the literature with practical guidance related to our specific implementation. It can be read as a lecture, or used to find the specific feature you need through the search function. We hope you find it useful.

Tip: Explore the bestiary!

The package contains many copula families. Classifying them is essentially impossible, since the class is infinite-dimensional, but the package proposes a few standard classes: elliptical, archimedean, extreme value, empirical...

Each of these classes more or less corresponds to an abstract type in our type hierarchy, and to a section of this documentation. Do not hesitate to explore the bestiary !

References

1. H. Joe. Multivariate Models and Multivariate Dependence Concepts (CRC press, 1997).

2. U. Cherubini, E. Luciano and W. Vecchiato. Copula Methods in Finance (John Wiley & Sons, 2004).

3. R. B. Nelsen. An Introduction to Copulas. 2nd ed Edition, Springer Series in Statistics (Springer, New York, 2006).

4. H. Joe. Dependence Modeling with Copulas (CRC press, 2014).

5. J.-F. Mai, M. Scherer and C. Czado. Simulating Copulas: Stochastic Models, Sampling Algorithms, and Applications. 2nd edition Edition, Vol. 6 of Series in Quantitative Finance (World Scientific, New Jersey, 2017).

6. F. Durante and C. Sempi. Principles of Copula Theory (Chapman and Hall/CRC, 2015).

7. C. Czado. Analyzing Dependent Data with Vine Copulas: A Practical Guide With R. Vol. 222 of Lecture Notes in Statistics (Springer International Publishing, Cham, 2019).

8. J. Größer and O. Okhrin. Copulae: An Overview and Recent Developments. WIREs Computational Statistics (2021).

9. A. Sklar. Fonctions de Repartition à n Dimension et Leurs Marges. Université Paris 8, 1–3 (1959).

10. T. Lux and A. Papapantoleon. Improved Fréchet-Hoeffding Bounds on $d$-Copulas and Applications in Model-Free Finance, arXiv:1602.08894 math, q-fin.

11. R. Kaas, J. Dhaene, D. Vyncke, M. J. Goovaerts and M. Denuit. A Simple Geometric Proof That Comonotonic Risks Have the Convex-Largest Sum. ASTIN Bulletin: The Journal of the IAA 32, 71–80 (2002).

12. L. Hua and H. Joe. Multivariate Dependence Modeling Based on Comonotonic Factors. Journal of Multivariate Analysis 155, 317–333 (2017).